关于leetcode环形链表相关题目的总结

发表于 | 分类于 |

引言

  • 这几天，博主总结了一些leetcode的链表题目，本文参考了网上大牛的文章，结合自己的想法，总结了环形链表的解决方案，欢迎各位补充／批评指正。

建模

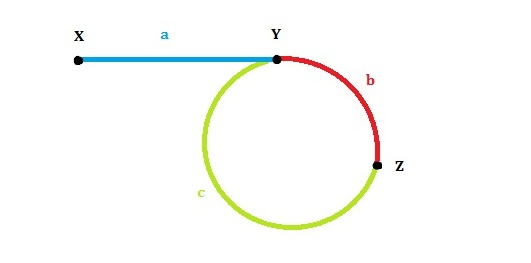
  • 链表头节点是X，环的第一个节点是Y;
  • slow和fast分别是指针，如果从链表头部开始往后移动，且fast指针移动速度为slow指针移动速度的两倍，设第一次的交点是Z；
  • 各段的长度分别是a,b,c，如图所示；
  • 环的长度是L；
  • slow和fast指针的向前移动速度分别是qs,qf；

roll

判断链表是否有环（leetcode 141）

  • fast如果走到了null，证明没有环；
  • fast如果和slow相遇了，证明有环；
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        
        while(fast!=null&&fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if(fast==slow){
                return true;
            }
        }
        return false;
    }
}

环长度是多少

  • 方法一：在第一次相遇后，相当于slow和fast的距离是一个环的长度，继续让这两个指针以各自的速度去走，下一次相遇时，走过的节点数即为环的长度；
  • 方法二：第一次相遇后，让fast停着不走了，slow继续走，记录到下次相遇时走过了几个节点，即为环的长度；
  • 方法三：第一次相遇时slow走过的距离：a+b，fast走过的距离：a+b+c+b；因为fast的速度是slow的两倍，所以fast走的距离是slow的两倍，有 2(a+b) = a+b+c+b；可以得到a=c；最终我们得到L=b+c=a+b，也就是说，从一开始到二者第一次相遇，循环的次数就等于环的长度；

找到环中的第一个节点（leetcode 142）

  • 我们已经得到了结论a=c；
  • 那么让两个指针分别从X和Z开始走，每次走一步，那么正好会在Y相遇，也就是环的第一个节点；
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while(fast!=null&&fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow==fast){
                fast = head;
                while(fast!=slow){
                    slow = slow.next;
                    fast = fast.next;
                }
                return slow;
            }
        }
        
        return null;
    }
}

如何将有环的链表变成单链表（解除环）

  • 在上一个问题的最后，将c段中Y点之前的那个节点与Y的链接切断即可；

如何判断两个单链表是否有交点，如何找到第一个相交的节点（leetcode 160）

  • 先判断两个链表是否有环；
  • 如果一个有环一个没环，肯定不相交；
  • 如果两个都没有环，判断两个列表的尾部是否相等；
  • 如果两个都有环，判断一个链表上的Z点是否在另一个链表上；
  • 找到第一个相交的节点方法：
    • 求出两个链表的长度L1,L2（如果有环，则将Y点当做尾节点来算）;
    • 假设L1<L2，用两个指针分别从两个链表的头部开始走;
    • 长度为L2的链表先走(L2-L1)步，然后两个一起走，直到二者相遇；
  • 代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public static int getLength(ListNode head){
        ListNode point = head;
        int length = 1;
        while(point!=null){
            length++;
            point = point.next;
        }
        
        return length;
    }
    
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        int aLength = getLength(headA);
        int bLength = getLength(headB);
        int diff = Math.max(aLength,bLength)-Math.min(aLength,bLength);
        
        ListNode pointA = headA;
        ListNode pointB = headB;
        
        while(diff>0){
            if(aLength>bLength){
                pointA = pointA.next;
            }else if(aLength<bLength){
                pointB = pointB.next;
            }
            diff--;
        }
        
        while(pointA!=pointB){
            pointA = pointA.next;
            pointB = pointB.next;
        }
        
        return pointA;
    }
}
您的支持是对我最大的鼓励！